BOIDS

14 Oct 2019 - val

What are boids? Boids are approximations for birds, fish and other animals (or things, really) exhibiting flocking behaviour, and are used for simulating just that. Boids behave according to certain rules. These are as follows:

• Cohesion: Boids will try to stay in the same area as their peers
• Seperation: Boids will not let anyone get too close
• Alignment: Boids will try to move in the same direction as their peers

I will implement this behaviour using Haskell, with gloss as the renderer. Now, let’s start by implementing a data structure.

The data structure

type Vector = (Float, Float)

data Boid = Boid { position     :: (Float, Float)
                 , velocity     :: (Float, Float)
                 , acceleration :: (Float, Float)
                 }

At first, I define a type alias Vector, which is really just a pair of 2 Numbers when working in 2D. I use this type to describe the movements of my boids.

Right now, we only store the position, velocity and acceleration of a boid (all as vectors), but I’m not sure we actually need to store acceleration. I am wondering because acceleration is the quantity we will be calculating based on the boids surroundings.

The data structure itself is written in record syntax. Check it out here if you have never seen it before. Next, I assign aliases to the getter functions generated by the record, for brevity’s sake.

Renderer

Now that we can store boids, lets display them!

DRAWING A BOID

We will display a boid as a simple triangular shape.

baseTriangle :: Picture
baseTriangle = Polygon [(8, 0), (-4, 4), (-3, 0), (-4, -4)]

drawBoid :: Boid -> Picture
drawBoid (Boid (x, y) _ a) = translate x y $ rotate angle $ color white baseTriangle
  where
    angle = (360 / (2 * pi)) * phase ihat a

drawBoids :: [Boid] -> Picture
drawBoids = pictures . map drawBoid

ihat :: Vector
jhat :: Vector
ihat = (1, 0)
jhat = (0, 1)

In order to test our function, we need a way to generate a bunch of Boids at once. At least, I wont type them out.

testBoids :: Float -> [Boid]
testBoids n = [makeBoidAtPos (x*10, y*10) | x <- [1..m], y <- [1..m] ]
  where
    m = n / 10

This fuction generates a grid of boids form (0, 0) to (n, n). Now lets feed that into drawBoids.

display FullScreen black $ translate (-960) (-540) $ drawBoids $ testBoids 100

Wonderful! We can see all our little boids, bunched up in the corner of the screen. If we zoom in, we can see the shape we defined. Also, we can clearly see that all boids face in the same direction, which makes sense, as all boids are generated with an acceleration of 0.

pos :: Boid -> Vector
pos = position

vel :: Boid -> Vector
vel = velocity

acc :: Boid -> Vector
acc = acceleration

Sticky

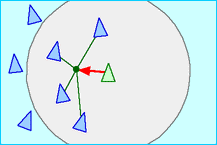
The rule of cohesion says that boids tend to cluster together. More accurately, the tend to follow the “center of mass” of their peers. This means that in order to implement cohesion, we need a function that can find the “center of mass”. Let’s call it findCenter. How creative.

MAN IN THE MIDDLE

This is how I implemented findCenter:

findCenter :: [Boid] -> Vector
findCenter boids = sum /> len
  where
    sum = (sumv . map pos) boids
    len = (fromIntegral . length) boids

Ok… and what does this do? Let’s start with the the two variables, sum and len.

sum is just the sum of all the position vectors of the boids that were passed to the function, while len is the amount of boids. In order to calculate sum, I implemented a new function sumv to sum vectors, with the self-defined +>, an operator to add two vectors.

sumv :: [Vector] -> Vector
sumv = foldl (+>) (0, 0)

(+>) :: Vector -> Vector -> Vector
(a, b) +> (c, d) = (a+c, b+d)

The last unknown is the /> operator. It divides any vector by a scalar.

(/>) :: Vector -> Float -> Vector
(a, b) /> c = (a/c, b/c)

COHESION

Now, how do we get our boid to actually move towards the center of mass of it and its peers? Simple. We subtract our the position vector of findCenter form our own (the boids own) position vector. This is the direction we want to move in, according to the rule of cohesion. ~> is simply vector subtraction.

cohesion :: Boid -> [Boid] -> Vector
cohesion b bs = findCenter bs ~> pos b

(~>) :: Vector -> Vector -> Vector
(a, b) ~> (c, d) = (a-c, b-d)

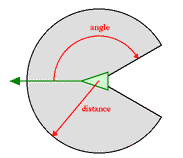
This should work fine, but in order for proper swarm-like behaviour to emerge, we can’t have our boids seeing every other boid. Therefore, we need a maximum view distance as well as a view angle – a field of view.

So we change out cohesion function like this:

cohesion :: Boid -> [Boid] -> Vector
cohesion b bs = findCenter peers ~> pos b
  where
    peers = filter (canView b) bs

Simple enough, right? Well, the entire complexity is hiding behind canView.

viewDist :: Float
viewDist = 100

viewAngleDeg :: Float -- from center to boder in degrees
viewAngleDeg = 70

viewAngleRad :: Float
viewAngleRad = viewAngleDeg * 2 * pi / 360

dist :: Vector -> Vector -> Float
dist (a, b) (c, d) = sqrt $ dx^2 + dy^2
  where
    dx = a - c
    dy = b - d

phase :: Vector -> Vector -> Float
phase u v = acos $ dotp / len
  where
    dotp = u .> v
    len = (lenv u) * (lenv v)

canView :: Boid -> Boid -> Bool
canView viewer subject
  | dist (pos viewer) (pos subject) > viewDist = False
  | abs ( phase (acc viewer) (pos subject ~> pos viewer) ) > viewAngleRad = False
  | otherwise = True

dist and phase can calculate the distance between two position vectors, or the pahse between two vectors, respectively. We need these to check whether or not a boid is withing our viewing range and field of view. Checking whether another boid is close enough to influence us is relatively simple – just perform dist on our position vectors. Checking for FOV is a bit harder though – we know that we need to calculate phase, but on what vectors?

The first vector should be our heading. To get that, we will just look at the acceleration of our boid (meaning that we actually do have to store it). The other vector should be the vector between us and the other boid. So we use our getter functions to access the relevant vectors and calculate away! By the way, .> is just a dot product operator.

Icky

On to the rule of separation!

SAFE SPACE

Every boid wants to keep a certain distance from other boids in order to avoid crashing. This is why we need a way to get all boids within our personal “safe space”.

boidsInSafeSpace :: Boid -> [Boid] -> [Boid]
boidsInSafeSpace b bs = filter (inSafeSpace b) bs
  where
    inSafeSpace subject suspect = dist (pos subject) (pos suspect) > safeSpace

GET AWAY!

Now that we know who is getting to close, we can figure out where to run to. Let’s write a function that takes two boids and returns a desired direction of movement.

escapeRoute :: Boid -> Boid -> Vector
escapeRoute escaper intruder = route /> (distance / safeSpace)
  where
    route = pos escaper ~> pos intruder
    distance = lenv route

We simply calculate the vector between the two boid position and scale it according to the distance between the boids – the closer another boid is, the faster a boid wants to get away.

SEPARATION

Using our new escapeRoute function, we can now implement seperation. At first, we get all boids inside our safe space, run escapeRoute on each one, and add up the escape vectors.

seperation :: Boid -> [Boid] -> Vector
seperation b = normalize . foldl (\ vector boid -> vector +> escapeRoute b boid) (0, 0)

Alignment

Last but not least – Alignment. I’ll make this quick. For this rule, we can reuse the canView function. The whole alignment calculation is pretty similar to the cohesion calculation. Instead of averaging positions, velocities are averaged. Then, we do not need to subtract anything, because we will just steer in that same direction.

alignment :: Boid -> [Boid] -> Vector
alignment boid boids = normalize $ sum /> len
  where
    peers = filter (canView boid) boids
    sum = (sumv . map vel) peers
    len = (fromIntegral . length) peers